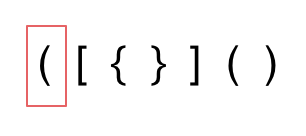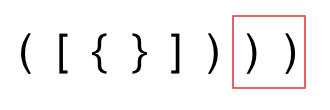栈的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
// 栈类
function Stack() {
    // 栈中的属性
    this.items = []

    // 栈中相关方法
    // push(element): 添加一个新元素到栈顶位置.

    // pop()：移除栈顶的元素，同时返回被移除的元素。

    // peek()：返回栈顶的元素，不对栈做任何修改（这个方法不会移除栈顶的元素，仅仅返回它）。

    // isEmpty()：如果栈里没有任何元素就返回true，否则返回false。

    // clear()：移除栈里的所有元素。

    // size()：返回栈里的元素个数。这个方法和数组的length属性很类似。

    Stack.prototype.push = function (element) {
        this.items.push(element)
    }

    Stack.prototype.pop = function () {
        return this.items.pop()
    }

    Stack.prototype.peek = function () {
        return this.items[this.items.length - 1]
    }

    Stack.prototype.isEmpty = function () {
        return this.items.length == 0
    }

    Stack.prototype.clear = function () {
        this.items = []
    }

    Stack.prototype.size = function () {
        return this.items.length
    }

    Stack.prototype.toString = function () {
        return this.items.join(" ")
    }

}

// 栈代码测试
var stack = new Stack()
stack.push(1)
stack.push(2)
// console.log(stack.size())
stack.size()

栈的应用

十进制转二进制

使用栈来存储循环除法的值，然后循环从栈顶取值就是该值的二进制。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
function dec2bin(decNumber) {
    var stack = new Stack()
    var remainder

    // 循环除法
    while (decNumber > 0) {
        remainder = decNumber % 2
        stack.push(remainder)
        // floor是向下取整
        decNumber = Math.floor(decNumber / 2)
    }

    console.log(stack.toString());

    // 从栈顶取值
    var binaryString = ''
    while(stack.size() > 0) {
        binaryString += stack.pop()
    }

    return binaryString
}

// 栈代码测试
var stack = new Stack()
stack.push(1)
stack.push(2)
// console.log(stack)
// stack.size()

// 转二进制
var test = dec2bin(235)
console.log(test);

(*)用两个栈实现队列

地址：232. 用栈实现队列 - 力扣（LeetCode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
var MyQueue = function() {
    this.stackIn = []
    this.stackOut = []
};

/** 
 * @param {number} x
 * @return {void}
 */
MyQueue.prototype.push = function(x) {
    this.stackIn.push(x)
};

/**
 * @return {number}
 */
MyQueue.prototype.pop = function() {
    const length = this.stackOut.length
    if(length) {
        return this.stackOut.pop()
    }
    // 将 stackIn 内的所有数据放入 stackOut 中
    while(this.stackIn.length) {
        this.stackOut.push(this.stackIn.pop())
    }
    return this.stackOut.pop()
};

/**
 * @return {number}
 */
MyQueue.prototype.peek = function() {
    // 调用原型上的 pop 方法
    // 相当于 MyQueue.prototype.pop
    const x = this.pop();
    // 因为pop函数弹出了元素res，所以再添加回去
    this.stackOut.push(x);
    return x;
};

/**
 * @return {boolean}
 */
MyQueue.prototype.empty = function() {
    return !this.stackIn.length && !this.stackOut.length
};

有效的括号

地址：20. 有效的括号 - 力扣（LeetCode）

题解参考代码随想录。

地址：代码随想录 (programmercarl.com)

由于栈结构的特殊性，非常适合做对称匹配类的题目。

首先要弄清楚，字符串里的括号不匹配有几种情况。

一些同学，在面试中看到这种题目上来就开始写代码，然后就越写越乱。

建议要写代码之前要分析好有哪几种不匹配的情况，如果不动手之前分析好，写出的代码也会有很多问题。

先来分析一下 这里有三种不匹配的情况，

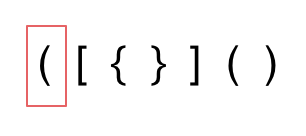
  1. 第一种情况，字符串里左方向的括号多余了 ，所以不匹配。 括号匹配1
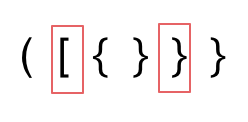
  2. 第二种情况，括号没有多余，但是 括号的类型没有匹配上。 括号匹配2
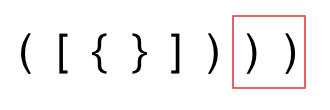
  3. 第三种情况，字符串里右方向的括号多余了，所以不匹配。 括号匹配3

我们的代码只要覆盖了这三种不匹配的情况，就不会出问题，可以看出 动手之前分析好题目的重要性。

动画如下：

20.有效括号

第一种情况：已经遍历完了字符串，但是栈不为空，说明有相应的左括号没有右括号来匹配，所以return false

第二种情况：遍历字符串匹配的过程中，发现栈里没有要匹配的字符。所以return false

第三种情况：遍历字符串匹配的过程中，栈已经为空了，没有匹配的字符了，说明右括号没有找到对应的左括号return false

那么什么时候说明左括号和右括号全都匹配了呢，就是字符串遍历完之后，栈是空的，就说明全都匹配了。

分析完之后，代码其实就比较好写了。

JS代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * @param {string} s
 * @return {boolean}
 */
var isValid = function(s) {
    // 用数组来模拟栈
    let stack = []
    // 用一个 map 来存 左括号和右括号
    // map 的构造函数可以将一个二维键值对数组转换成一个 Map 对象
    let map = new Map([
        ['(', ')'],
        ['{', '}'],
        ['[', ']']
    ])
    for(let i = 0; i < s.length; i++) {
        // 匹配到左括号，将对应的右括号放入栈中
        if(map.has(s[i])) {
            stack.push(map.get(s[i]))
        } else {
            // 匹配到的是右括号, 右括号必须和此时栈顶的元素一致，不一致就返回false 
            let x = stack.pop();
            if(x !== s[i]) {
                return false
            }
        }
    }
    // 遍历结束后，如果栈为空，说明全匹配
    return stack.length === 0
};

删除字符串中的所有相邻重复项

地址：1047. 删除字符串中的所有相邻重复项 - 力扣（LeetCode）

这题的思路和上面的匹配括号一致，掌握上一题，这一题就很简单。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/**
 * @param {string} s
 * @return {string}
 */
var removeDuplicates = function(s) {
    // 还得是栈来解决
    let stack = []
    for(let i = 0; i < s.length; i++) {
        // 取栈顶的数据
        let x = stack[stack.length - 1];
        // 相同就出栈
        if(x == s[i]) {
            stack.pop()
        } else {
            // 不同就入栈
            stack.push(s[i])
        }
    }
    return stack.join('')
};

逆波兰表达式求值

地址：150. 逆波兰表达式求值 - 力扣（LeetCode）

思路：看个图

150.逆波兰表达式求值

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
/**
 * @param {string[]} tokens
 * @return {number}
 */
var evalRPN = function(tokens) {
    // 还得是栈来解决
    // 便利数组到运算符，从栈顶取两个数，用这个运算符进行运算，然后将运算后的值再压入栈
    // 用一个 set 来存运算符
    let set = new Set(['*', '/', '+', '-'])
    // stack 来模拟栈
    let stack = []
    for(let i = 0; i < tokens.length; i++) {
        // 判断是否是运算符
        if(set.has(tokens[i])) {
            // 从栈顶取两个数值进行运算
            let y = stack.pop()
            let x = stack.pop()
            let result = 0
            // 用此运算符进行运算
            switch(tokens[i]) {
                case '*':
                    result = x * y;
                    break;
                case '/':
                    // '/' 要向下取值
                    // 判断正负
                    if(x / y > 0) {
                        result = Math.floor(x / y);
                    } else {
                        result = Math.ceil(x / y)
                    }
                    break;
                case '+':
                    // 将字符串转成数字 
                    result = x + y;
                    break;
                case '-':
                    result = x - y;
                    break;
            }
            // 将运算结果存入栈
            stack.push(result)
        } else {
            // 不是运算符就存入栈
            stack.push(+tokens[i])
        }
    }
    return stack.pop()
};

队列的实现

普通队列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
// 队列
function Queue() {
    // 队列数据
    this.items = []

    // enqueue(element)：向队列尾部添加一个（或多个）新的项。
    Queue.prototype.enqueue = function (element) {
        this.items.push(element)
    }

    // dequeue()：移除队列的第一（即排在队列最前面的）项，并返回被移除的元素。
    Queue.prototype.dequeue = function () {
        return this.items.shift()
    }

    // front()：返回队列中第一个元素——最先被添加，也将是最先被移除的元素。
    Queue.prototype.front = function () {
        return this.items[0]
    }

    // isEmpty()：如果队列中不包含任何元素，返回true，否则返回false。
    Queue.prototype.isEmpty = function () {
        return this.items.length == 0
    }

    // size()：返回队列包含的元素个数，与数组的length属性类似。
    Queue.prototype.size = function () {
        return this.items.length
    }
}

优先队列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
function PriorityQueue() {
    this.items = []

    // 封装一个新的构造函数，用来存元素和元素优先级
    function QueueElement(element,priority) {
        this.element = element
        this.priority = priority
    }

    // 添加元素的方法
    PriorityQueue.prototype.enqueue = function (element,priority) {
        var queueElement = new QueueElement(element,priority)

        if (this.isEmpty()) {
            // 第一个数据
            this.items.push(queueElement)
        } else {
            // 要比较，然后插入到合适的位置
            var added = false
            for(var i = 0;i < this.items.length;i++) {
                if (this.items[i].priority > queueElement.priority) {
                    // 插在这个元素的前面
                    this.items.splice(i,0,queueElement)
                    // 添加成功
                    added = true
                    break
                }
            }

            // 循环结束后都没有插到前面，说明就是要放在最后一位
            if (!added) {
                this.items.push(queueElement)
            }
        }      
    } 


    // dequeue()：移除队列的第一（即排在队列最前面的）项，并返回被移除的元素。
    PriorityQueue.prototype.dequeue = function () {
        return this.items.shift()
    }

    // front()：返回队列中第一个元素——最先被添加，也将是最先被移除的元素。
    PriorityQueue.prototype.front = function () {
        return this.items[0]
    }

    // isEmpty()：如果队列中不包含任何元素，返回true，否则返回false。
    PriorityQueue.prototype.isEmpty = function () {
        return this.items.length == 0
    }

    // size()：返回队列包含的元素个数，与数组的length属性类似。
    PriorityQueue.prototype.size = function () {
        return this.items.length
    }
}

队列的应用

约瑟夫环

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
// 约瑟夫环问题

var queue = new Queue()
queue.enqueue('lily')
queue.enqueue('lucy')
queue.enqueue('tom')
queue.enqueue('lilei')
queue.enqueue('why')
// queue.enqueue(6)

var count = 0;
while (queue.size() > 1) {
    // 因为数到3的就直接要出去，所以先上来直接数
    count++;
    if (count == 3) {
        queue.dequeue();
        count = 0;
    } else {
        // 这一部分只有不为3的时候才进行，之前错在了不管count是否为3，都执行。
        var temp = queue.dequeue();
        queue.enqueue(temp);
    }

}
console.log(queue.front());

(*)用队列实现栈

地址：225. 用队列实现栈 - 力扣（LeetCode）

思路：如图

225.用队列实现栈

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
var MyStack = function() {
    this.queueIn = []
    this.queueOut = []
};

/** 
 * @param {number} x
 * @return {void}
 */
MyStack.prototype.push = function(x) {
    this.queueIn.push(x)
};

/**
 * @return {number}
 */
MyStack.prototype.pop = function() {
    let temp = null
    this.queueOut = []
    while(this.queueIn.length - 1) {
        temp = this.queueIn.shift();
        this.queueOut.push(temp)
    }
    temp = this.queueIn.shift()
    this.queueIn = [...this.queueOut]
    return temp
};

/**
 * @return {number}
 */
MyStack.prototype.top = function() {
    let temp = null
    this.queueOut = []
    while (this.queueIn.length) {
        temp = this.queueIn.shift();
        this.queueOut.push(temp);
    }
    this.queueIn = [...this.queueOut];
    return temp;
};

/**
 * @return {boolean}
 */
MyStack.prototype.empty = function() {
    return this.queueIn.length === 0
};

(*)滑动窗口最大值

地址：239. 滑动窗口最大值 - 力扣（LeetCode）

这题要使用单调队列，设计的还是挺巧妙的，也不难。

题解：代码随想录 (programmercarl.com)

239.滑动窗口最大值-2

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
/**
 * @param {number[]} nums
 * @param {number} k
 * @return {number[]}
 */
var maxSlidingWindow = function(nums, k) {
    // 构造一个单调队列
    class MonoQueue {
        queue;
        constructor() {
            this.queue = []
        }
        // 进入队列
        // 规则：如果push的元素value大于入口元素的数值，那么就将队列入口的元素弹出，直到push元素的数值小于等于队列入口元素的数值为止
        enqueue(value) {
            let temp = this.queue[this.queue.length - 1]
            while(value > temp && temp != undefined) {
                // 出队
                this.queue.pop()
                temp = this.queue[this.queue.length - 1]
            }
            this.queue.push(value)
        }
        // 出队列
        // 规则：如果窗口移除的元素value等于单调队列的出口元素，那么队列弹出元素，否则不用任何操作
        dequeue(value) {
            if(value === this.front()) {
                // 弹出元素
                this.queue.shift()
            }
        }
        // 返回队首第一个元素
        front() {
            return this.queue[0]
        }
    }

    // 开始滑动窗口
    // 先放入前 n 个进队列
    let queue = new MonoQueue()
    // 用来存放最大值
    let result = []
    for(let i = 0; i < k; i++) {
        queue.enqueue(nums[i])
    }
    result.push(queue.front())
    // 开始滑动
    for(let i = k; i < nums.length; i++) {
        // 进队
        queue.enqueue(nums[i])
        // 出队
        queue.dequeue(nums[i - k])
        // 滑动
        result.push(queue.front())
    }
    return result
};

前K个高频元素（TODO）

地址：代码随想录 (programmercarl.com)

这题要用到堆，大顶堆，小顶堆还没复习到，先暂时跳过